No post anterior, Os 12 passos para calcular a espessura mínima de um tubo reto de aço inoxidável conforme normas ASME B31.3 (Equação 3a), vimos como determinar a espessura mínima de um tubo reto de aço inoxidável conforme o ASME B31.3, utilizando a Equação (3a), para um caso real de 60 bar (6 MPa) e 80 °C.
Esse cálculo é o ponto de partida de praticamente todo projeto de tubulação.
Mas, na prática, quase nenhuma linha é totalmente reta.
Curvas, desvios e mudanças de direção fazem parte da realidade da fábrica — e é exatamente por isso que o código dedica um item específico ao tema: o 304.2 – Curvas e Curvas de Gomo (Curved and Mitered Segments of Pipe)
Neste post, vamos entender o que muda no dimensionamento quando o tubo deixa de ser reto, com foco em curvas fabricadas a partir do próprio tubo, que é o cenário típico da tubulação sanitária em aço inox.
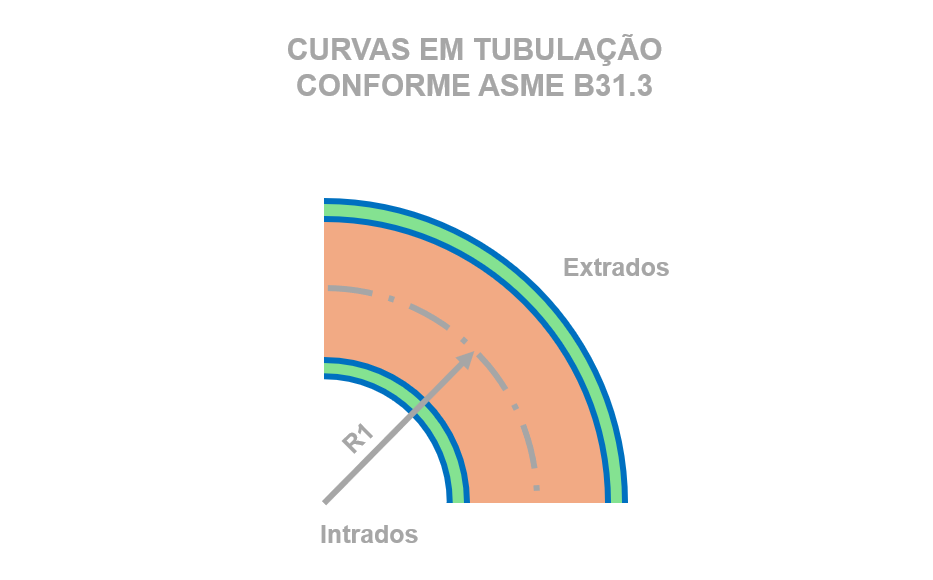
1. O ponto de partida continua sendo o tubo reto
A primeira coisa que precisa ficar clara é:
O ASME B31.3 não cria uma nova equação de pressão para curvas.
A espessura mínima por pressão:
- continua sendo calculada pelo item 304.1
- continua usando a Equação (3a)
- continua dependendo de P, D, S, E, W e Y
Ou seja, a curva nasce de um tubo que já foi corretamente dimensionado.
Exemplo base do post anterior
- Pressão de projeto: 60 bar (6 MPa)
- Temperatura: 80 °C
- Tubo: 2” OD (50,8 mm)
- Material: Aço inox TP304L
- Norma: ASTM A269
- Espessura mínima por pressão (tubo reto): já determinada no post anterior
Até aqui, nada muda.
2. Então por que o código separa tubo reto e curva?
Porque, mecanicamente, um tubo curvado não se comporta como um tubo reto.
Durante o processo de curvamento, ocorrem fenômenos importantes:
- ovalização da seção
- afinamento da parede no extrados (lado externo da curva)
- espessamento no intrados (lado interno)
- redistribuição das tensões na parede
O resultado prático é simples:
A espessura que governa a resistência da curva é a menor espessura após a curvatura — normalmente no extrados.
É exatamente isso que o código quer garantir.
3. Como o ASME B31.3 trata curvas (Seção 304.2)
O item 304.2 parte de um princípio claro:
Uma curva é aceitável se, após a curvatura, a espessura mínima da parede ainda atender à espessura exigida por pressão.
Ou seja:
- o cálculo de pressão não muda
- o critério de verificação muda
A norma deixa explícito que:
- a espessura mínima deve ser atendida após a curvatura
- o processo de fabricação passa a ser parte do problema de engenharia
4. 304.2.1 – Curvas em Tubulação (Pipe Bends): Introdução do fator geométrico
Para curvas fabricadas a partir do próprio tubo (pipe bends), o ASME B31.3 introduz o fator geométrico de curvatura I, que corrige o cálculo da espessura mínima conforme a posição analisada na curva.
A espessura mínima requerida após a curvatura, no acabamento final, é dada pela Equação (3c):
Onde:
- t = espessura mínima requerida após a curvatura
- P = pressão interna de projeto
- D = diâmetro externo do tubo
- S, E, W, Y = mesmos parâmetros do tubo reto
- I = fator geométrico de curvatura
5. Como calcular o fator I
O valor de I depende da posição considerada na curva.
Intrados (raio interno da curva)
Extrados (raio externo da curva)
Linha neutra (raio da linha de centro)
Onde:
- Intrados = raio de curvatura da curva
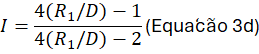
- Extrados = diâmetro externo do tubo
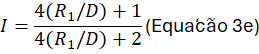
- Linha neutra (raio da linha de centro)
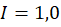
Onde:
- R1 = raio de curvatura da curva
- D = diâmetro externo do tubo
Como regra prática:
- o extrados governa, pois resulta em I < 1
6. Exemplo numérico – continuidade direta do tubo reto (60 bar)
Vamos manter exatamente o mesmo exemplo da série.
Dados
- P = 6 Mpa (60 bar)
- D = 50,8mm
- S = 115 Mpa
- E = 0,8
- W = 1,0
- Y = 0,4
Assumindo uma curva sanitária típica:
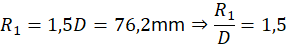
Fator I
- Intrados:
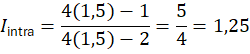
- Extrados:
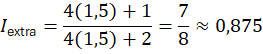
Espessura mínima requerida no extrados
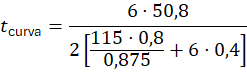
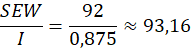
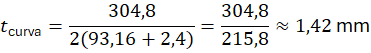
7. Interpretação correta do resultado
No post do tubo reto, a espessura mínima requerida por pressão foi da mesma ordem de grandeza.
Isso mostra algo fundamental:
Para curvas com raio adequado, o tubo reto continua governando o dimensionamento por pressão.
O §304.2 não existe para aumentar espessura automaticamente, mas para garantir que:
- a curvatura
- o afinamento
- e a geometria
não violem o dimensionamento já feito pelo 304.1.
8. Curva de tubo × cotovelo comercial (304.2.2)
Sistemas industriais em geral
- utilizam cotovelos comerciais
- normalizados (ex.: ASME B16.9)
- com espessura própria e classificação de pressão
Tubulação sanitária em aço inox
- curvas são fabricadas a partir do próprio tubo
- não existe “classe de pressão do cotovelo”
- o controle de espessura após a curvatura é crítico
Na tubulação sanitária, a curva não é um componente separado — ela é o próprio tubo deformado.
9. O que não se aplica à tubulação sanitária
O item 304.2.3 – Miter Bends trata de curvas segmentadas.
Embora previstas no código:
- raramente são usadas em sistemas sanitários
- criam descontinuidades geométricas
- dificultam limpeza, drenagem e inspeção
Por isso, não fazem parte do escopo desta série.
10. Checklist prático para curvas em aço inox sanitário
Antes de aprovar uma curva, verifique:
- o tubo atende ao 304.1?
- o raio de curvatura é adequado onde curvas de raio longo R=1,5D (Padrão OD) e outros raios conforme necessário?
- A espessura do seu extrado após fabricação não ultrapasse a espessura calculada?
Se sim, a curva atende ao ASME B31.3.
Conclusão
Curvar um tubo não muda a pressão interna, mas muda a forma como a parede resiste a ela.
O ASME B31.3 trata isso de forma clara:
- o cálculo da espessura continua sendo o do tubo reto
- a curva precisa provar que ainda atende após a deformação
Entender esse raciocínio evita dois erros comuns:
- superdimensionar sem necessidade
- ou, pior, aceitar uma curva que não atende à espessura mínima exigida
No próximo post da série, avançaremos para o item 304.3 – Derivações (Branch Connections), onde o tubo deixa de ser apenas curvado e passa a ser perfurado, introduzindo um novo desafio estrutural.
Bela abordagem, precisamos ficar atentos à esses detalhes.